Short two-qubit pulse sequences for exchange-only spin qubits in 2D layouts
(under review)
University of Chicago
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
University of Chicago
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
University of Chicago
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Intel Corporation
Abstract
Spin qubits in quantum dots offer an expansive design landscape for architecting scalable device layouts. Two exchange-only (EO) qubits can be connected in many ways, but the study of two-EO-qubit operations has so far been limited to a small number of the possible configurations, and previous works lack analyses of design considerations and implications for quantum error correction. We develop a simple method to efficiently find the optimal mapping of a fixed all-to-all pulse sequence to any restricted dot connectivity. We provide complete pulse sequences for CX, CZ, iSWAP, leakage-controlled CX, and leakage-controlled CZ two-qubit gates on 450 unique planar six-dot topologies and analyze differences in sequence length (up to 43\% reduction) across topology classes. In addition, we show that relaxing constraints on post-operation spin locations can yield further reductions in sequence length; conversely, constraining these locations in a particular way generates a CXSWAP operation with almost no additional cost over a standard CX. We experimentally verify pulses sequences for different operations in a linear-connectivity device and confirm that they work as expected. Finally, we explore architectural implications of these results for quantum error correction. Our work guides hardware and software design choices for future implementations of scalable quantum dot architectures.
[.pdf] [arXiv]Selected Figures
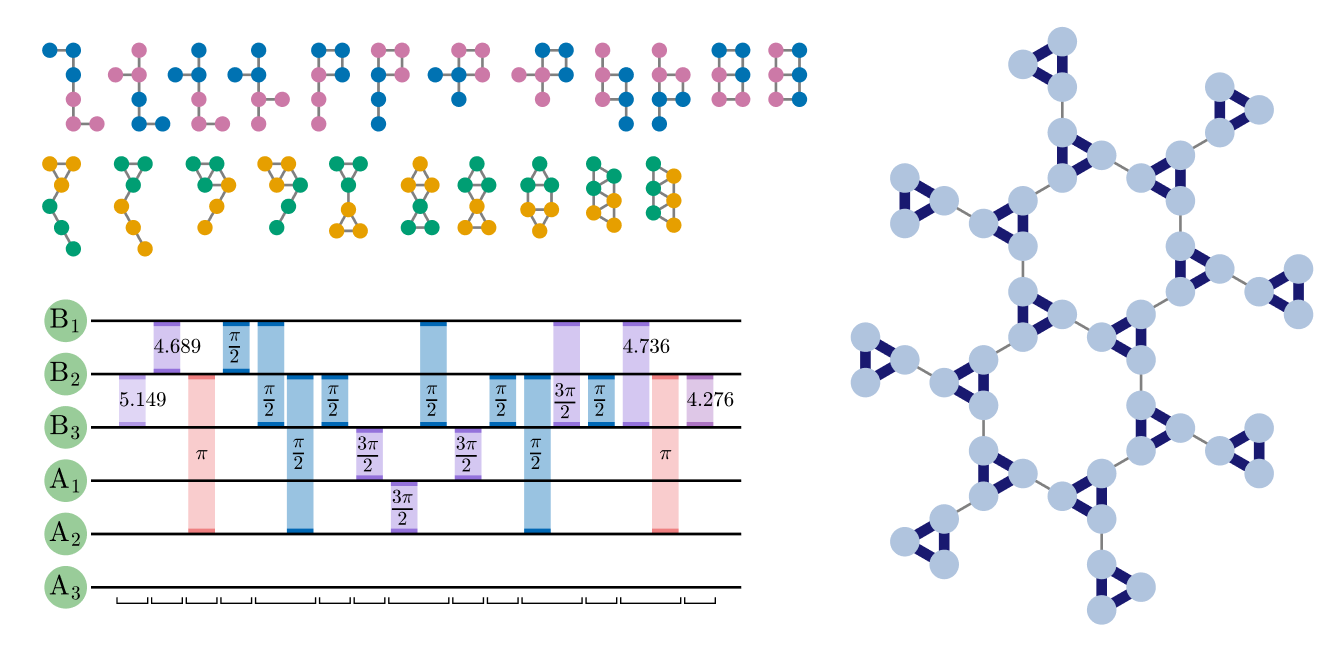
Figure 1. A 16-pulse sequence implementing a CX gate on two exchange-only qubits encoded in six spins, obtained by adding local corrections to the 12-pulse sequence from [36]. Each dot is labeled according to its qubit (A or B) and spin index, with gauge spins labeled A3 and B3. Each pulse is a partial swap operation between two spins [24], which can be implemented with the exchange interaction [22]. Brackets underneath show groups of sequential pulses which act on disjoint dots, and thus can in principle be applied in parallel. A different choice of local corrections can instead yield CZ; see Appendix A.
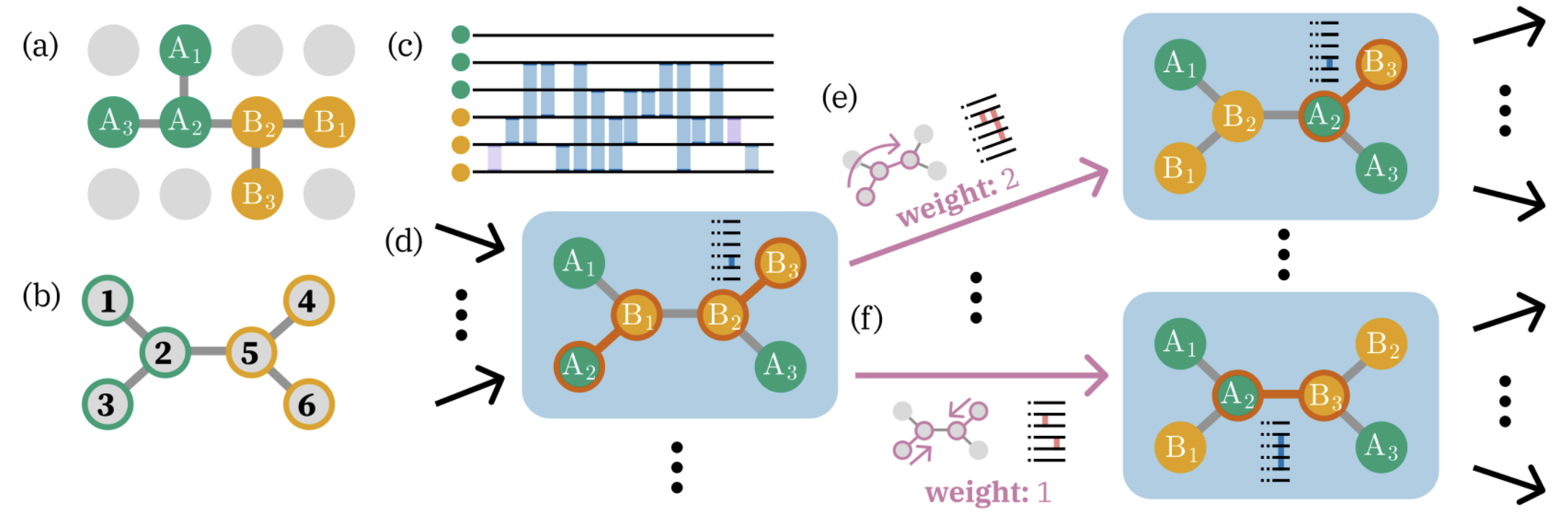
Figure 3. The optimization graph used to find a pulse sequence for a given dot configuration, described in Section III B 2. (a) Configuration of the two EO qubits of interest within a larger 2D grid of dots, with labeled spins comprising qubits A and B. Allowed exchange interactions are indicated by lines between dots. (b) Connectivity of the selected (numbered) dots, encoding the allowed exchange interactions. (c) Ideal all-to-all CX pulse sequence (assuming any exchange interaction is allowed). Not all of these edges are present in the connectivity of interest, so spin swaps must be interleaved to shuffle the spins between dots and bring the desired spins into contact. (d) A node of the optimization graph. Each node corresponds to the application of one of the reference pulses from the all-to-all sequence. At this layer, the pair $(B_2, B_3)$ is applied, so $B_2$ and $B_3$ must be in neighboring dots. Note the highlighted dot pairs $(A_2, B_1)$ and $(B_2, B_3)$ in red, corresponding to the most-recently-applied pulses. (e) An edge between nodes represents the insertion of spin-swap operations (exchange interactions). In this case, we perform spin swaps to move spin $A_2$ from dot 3 to dot 5, where it can interact with $B_3$ as desired. The weight of this edge is the total number of new pulses that will be added to the sequence: the first spin swap on dots (2,3) can be absorbed the previous pulse $(A_2, B_1)$; however, the second spin swap and the $(A_2, B_3)$ reference pulse each add one to the sequence length, so the overall edge weight is 2. (f) An edge to a different node in the next layer. In this case, we apply two spin swaps which can both be absorbed into previous pulses. The weight is 1 due to the $(A_2, B_3)$ pulse that is applied in the next node.
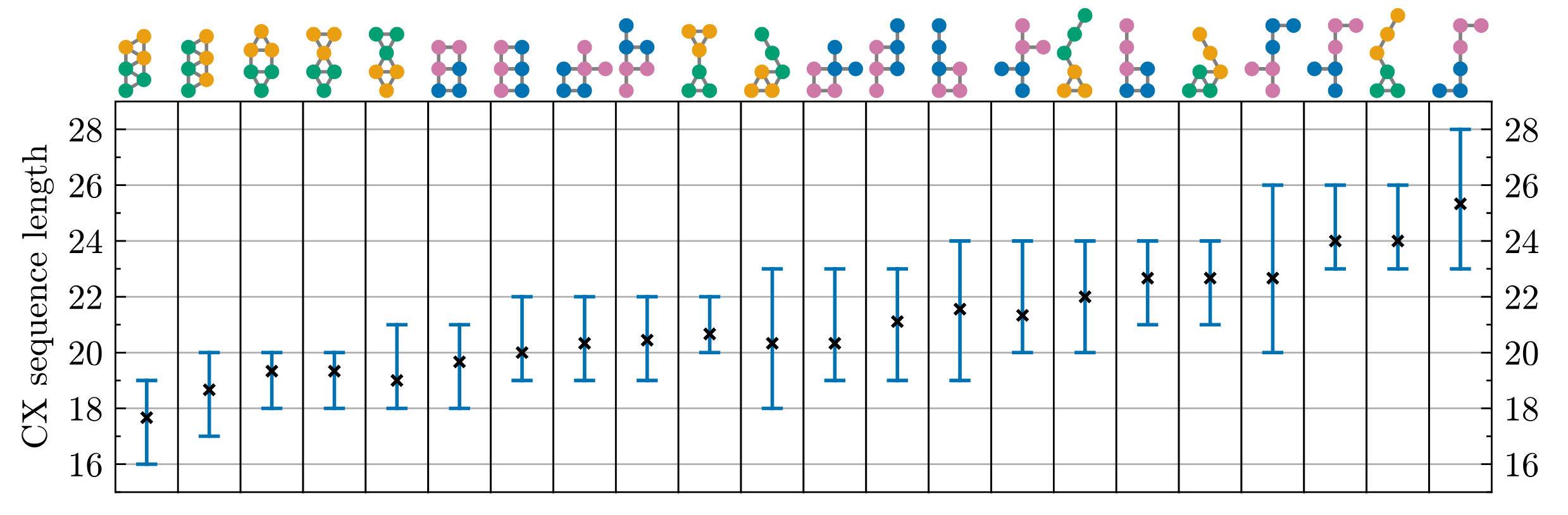
Figure 4. Optimized CX sequence lengths, grouped by permutation equivalence class. Within each class, blue line spreads from minimum to maximum sequence length and black x denotes mean. For rectangular-grid topologies, dark blue represents the “control” qubit of the CX and light purple the “target”. For non-rectangular-grid topologies, dark green represents the “control” and gold the “target”.
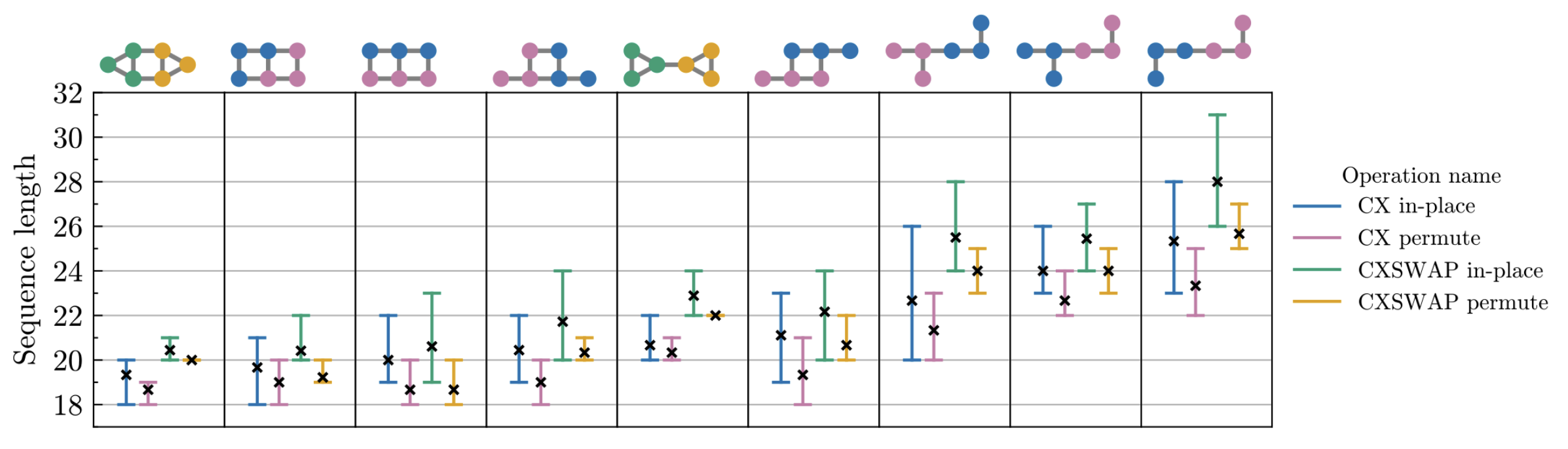
Figure 6. CX and CXSWAP sequence lengths for selected permutation equivalence classes, with and without intra-qubit spin permutations allowed. Across all topologies, CXSWAP is 22.2% shorter than applying CX and SWAP operations sequentially and is only 7.34% longer on average than CX. For both CX and CXSWAP, allowing permutations reduces the average and maximum sequence length within each equivalence class.
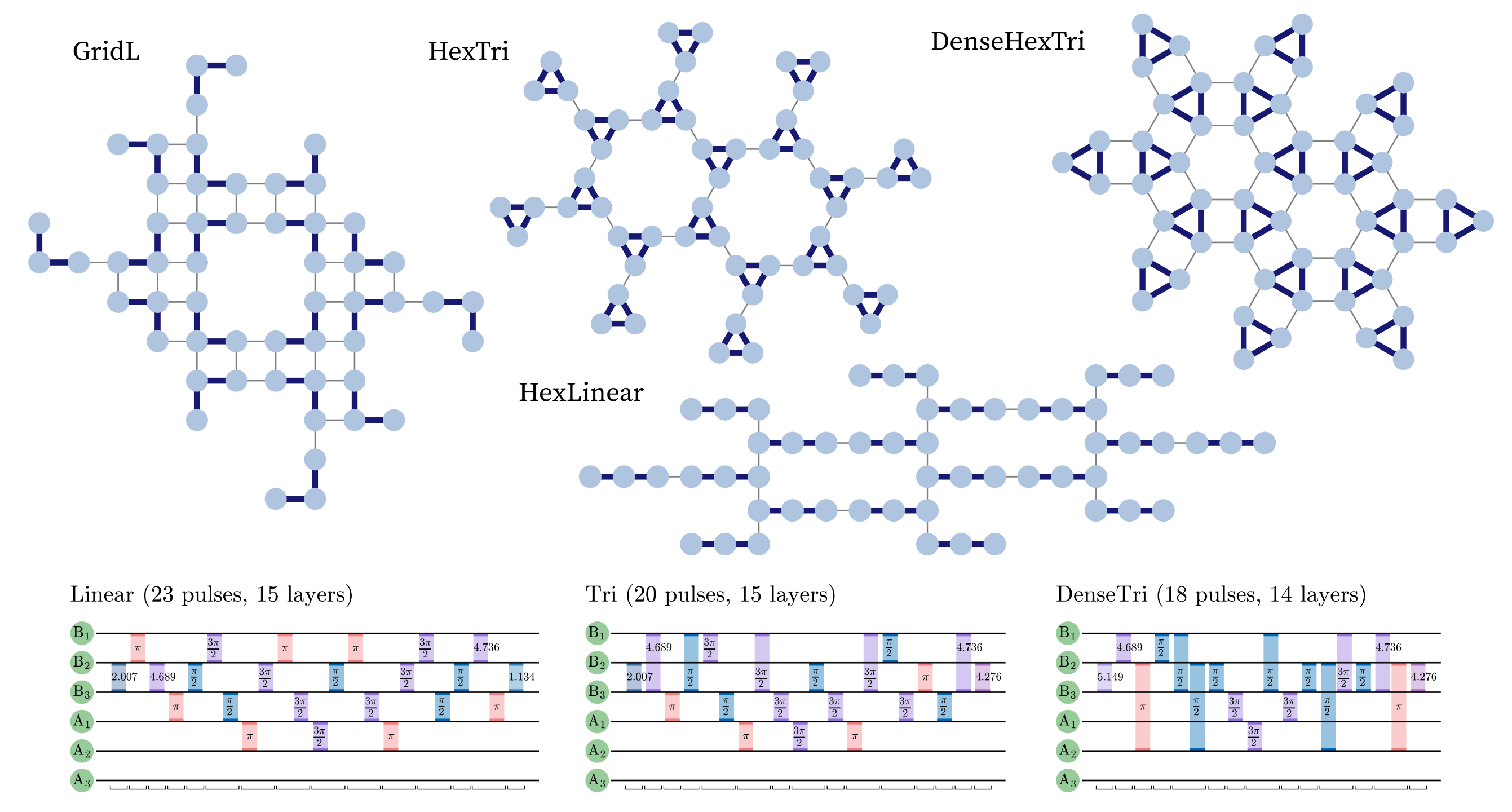
Figure 8. Top: The four dot layouts considered in this study. Names denote the qubit-level connectivity (Grid or Hex) and the dot-level connectivity (Linear, L, Tri). Thick dark blue lines indicate intra-qubit connections and thin gray lines indicate inter-qubit connections. Bottom: Example CX pulse sequences for three different two-EO-qubit connectivities. More densely-connected qubits yield shorter pulse counts (23 for Linear vs. 18 for DenseTri); however, note that the number of fully-parallel layers (14-15) remains similar.
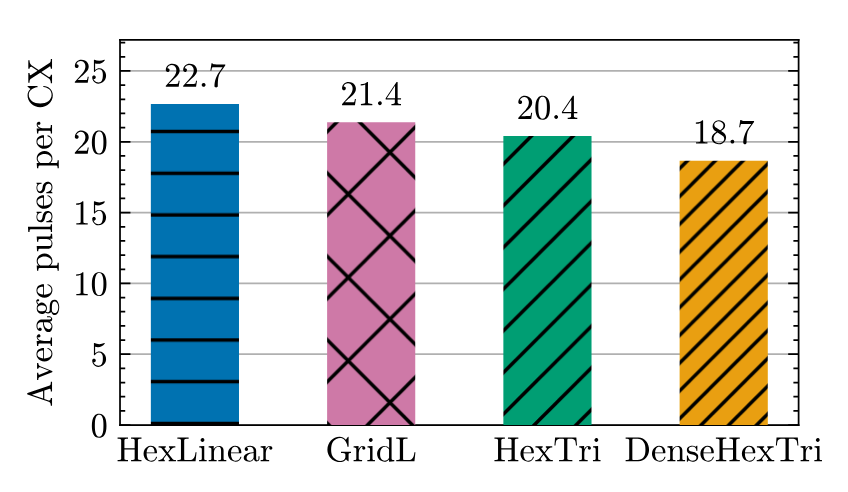
Figure 9. Average pulse count per CX for QEC round on each layout. As expected, more densely-connected layouts yield shorter pulse sequences.
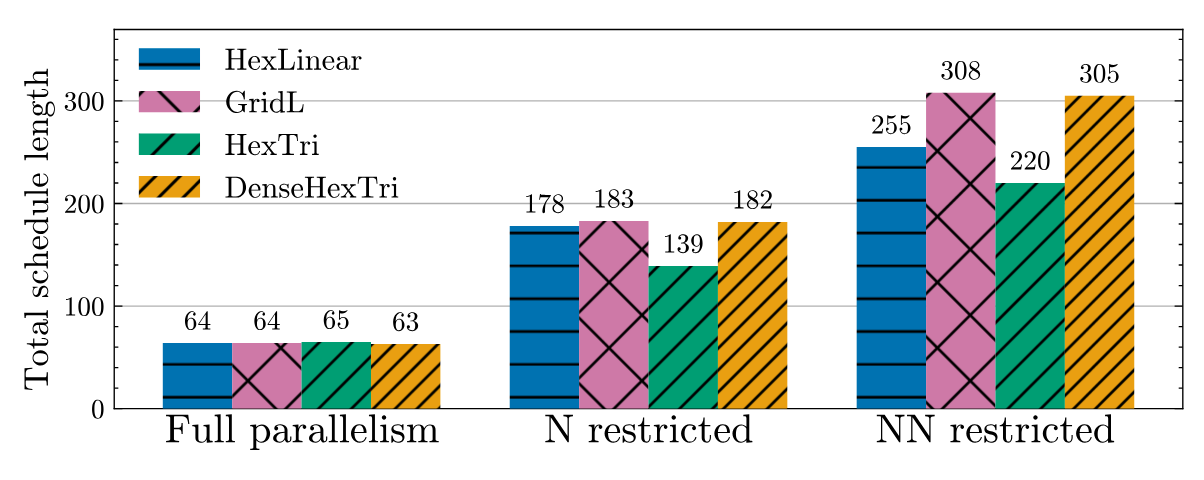
Figure 10. Schedule length for one full QEC cycle of CX gates, under various parallelism restrictions. Here, “length” refers to the duration of the schedule in terms of the number of steps, where many pulses can be applied in parallel during each step.
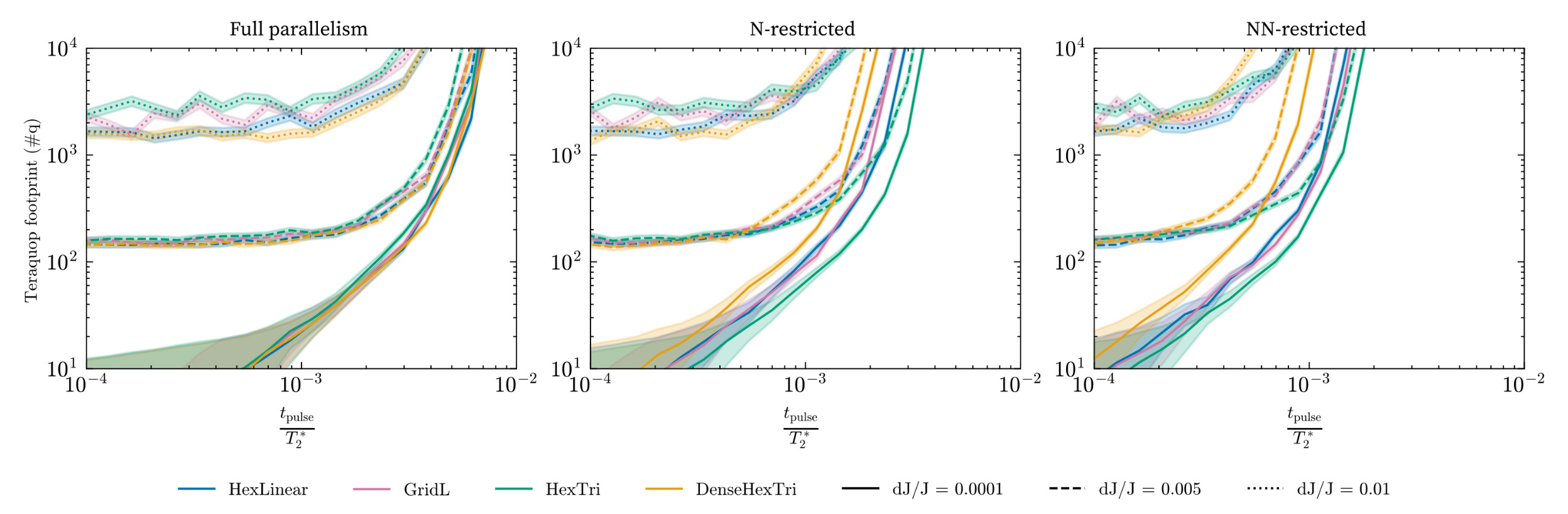
Figure 11. Teraquop footprints for all four layouts, under different parallelism conditions and in different noise regimes. $\frac{t_{\text{pulse}}}{T_2^*}$ varies along the x axis and each plot contains three groups of lines corresponding to different $\delta_J$ amounts.
My Contributions
Things I Learned
← back to jason-chadwick.com