Averting multi-qubit burst errors in surface code magic state factories
QCE 2024



University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
Abstract
Fault-tolerant quantum computation relies on the assumption of time-invariant, sufficiently low physical error rates. However, current superconducting quantum computers suffer from frequent disruptive noise events, including cosmic ray impacts and shifting two-level system defects. Several methods have been proposed to mitigate these issues in software, but they add large overheads in terms of physical qubit count, as it is difficult to preserve logical information through such a large error event.
We focus on mitigating multi-qubit burst errors in magic state factories, which are expected to comprise up to 95% of the spacetime cost of future quantum programs. Our key insight is that magic state factories do not need to preserve logical information over time; once we detect an increase in local physical error rates, we can simply turn off parts of the factory that are affected, re-map the factory to the new chip geometry, and continue operating. This is much more efficient than previous general methods that attempt to preserve the information encoded within logical qubits, and is resilient even under many simultaneous impact events. Using precise physical noise models, we show an efficient ray detection method and evaluate our strategy in different noise regimes. Compared to the best existing baselines, we find reductions in ray-induced overheads by several orders of magnitude, yielding reductions in total qubitcycle cost by geomean 6.5x to 13.8x depending on the noise model. This work reduces the burden on hardware by providing low-overhead software mitigation of these errors.
[.pdf] [publication] [arXiv] [slides] [code]Selected Figures
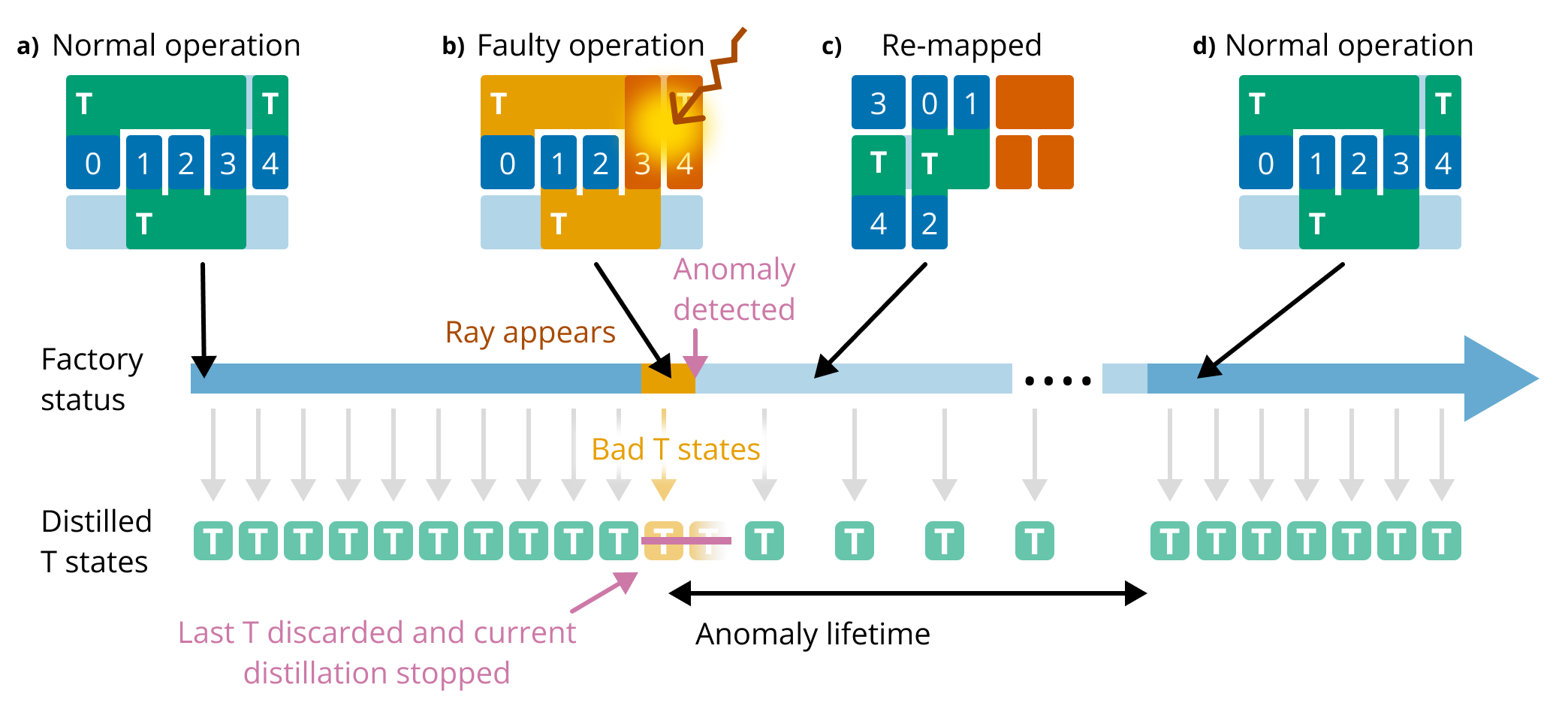
Figure 1. Overview of our method, showing the timeline of a magic state factory before and after a cosmic ray event. (a) The factory is operating normally. (b) A cosmic ray hits the chip, severely affecting physical qubit error rates nearby and causing the factory to output low-quality magic states. (c) The cosmic ray is detected after some delay. The distilled magic states in the buffer (yellow) are discarded, the affected physical qubits are turned offline, and the factory is re-mapped to avoid using the offline areas. The factory can continue to operate at reduced speed. (d) The affected physical qubits recover from the ray impact and are turned back online. The factory resumes normal operation.
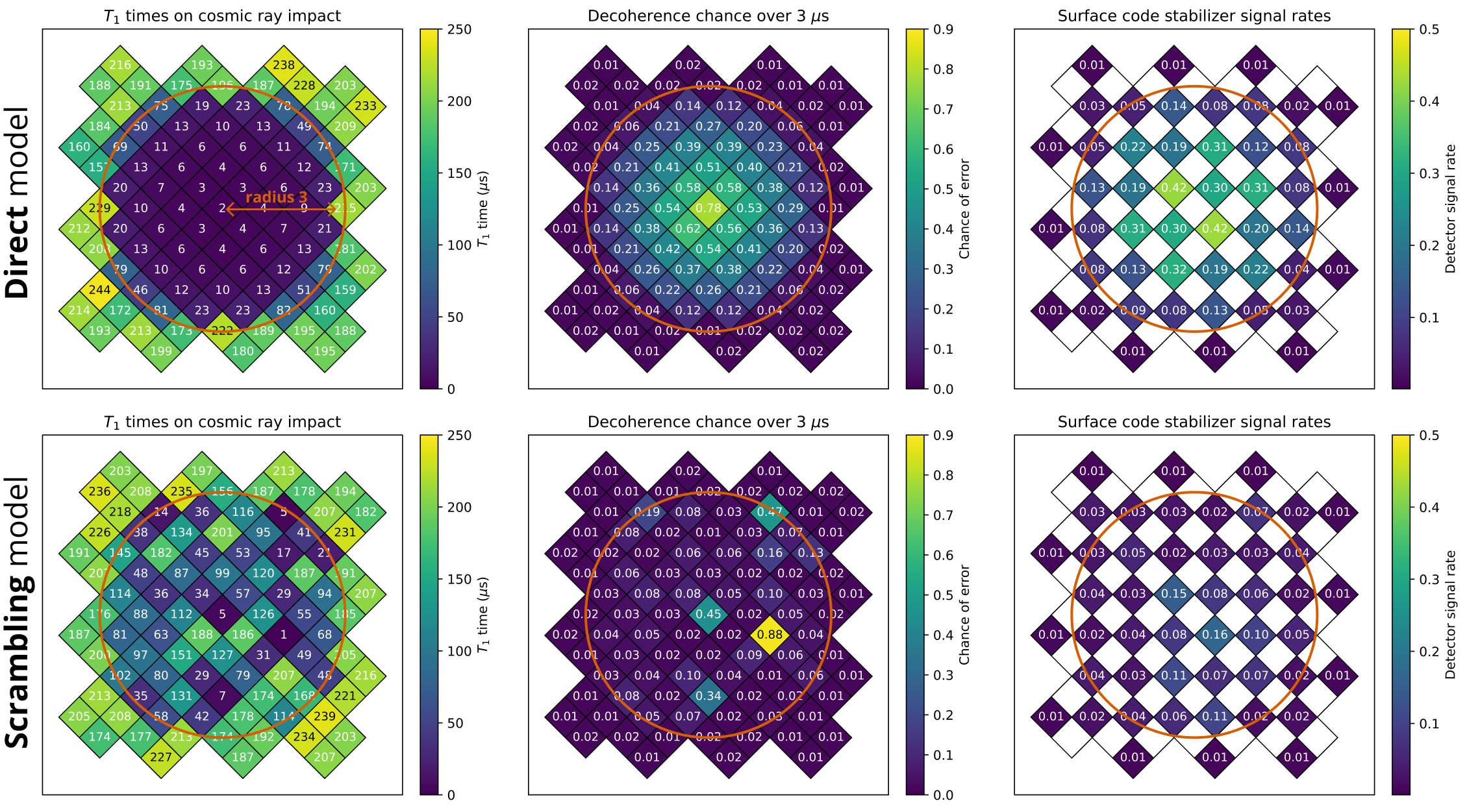
Figure 3. The two cosmic ray noise models studied in this work. From left to right, we show the effect of a representative ray on the physical qubit $T_1$ times, the decoherence error rate over $3\mu$s (the time period used in [23]), and the chance that each surface code stabilizer measurement will detect an error. Top: The Direct model is based on [23]. A ray impact directly affects the $T_1$ times of qubits within some radius, becoming less severe with distance. Bottom: The Direct model is based on [22], [44]. A ray impact scrambles TLS defects in some area, leading to unpredictable and long-lasting effects on qubit coherence.
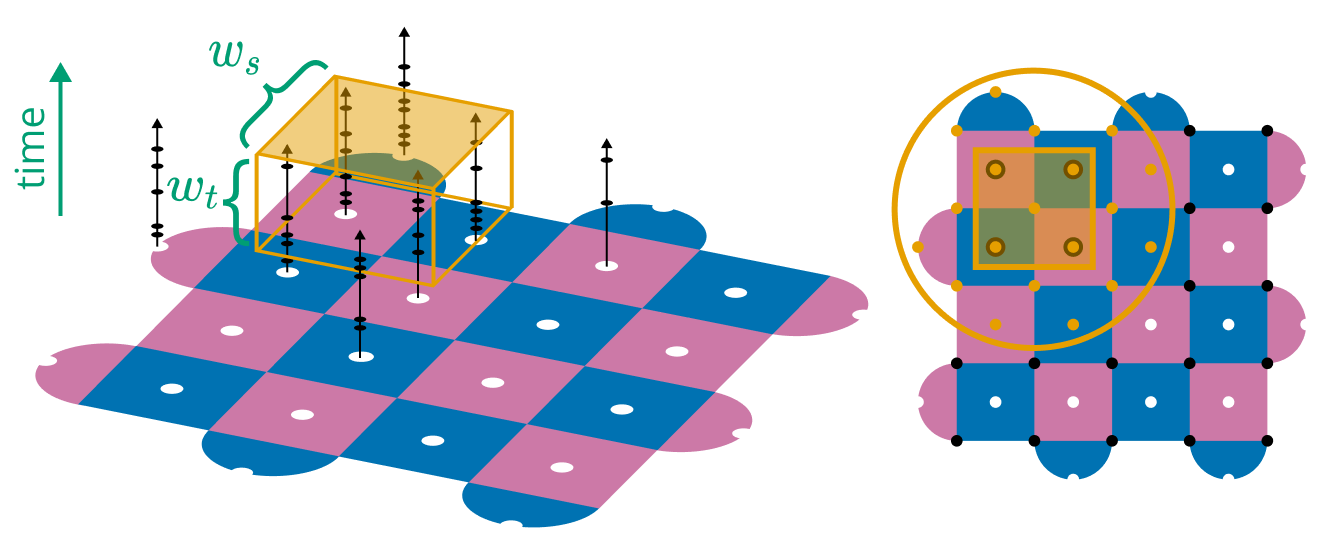
Figure 4. We detect cosmic rays by counting stabilizer syndromes in spatiotemporal windows. Left: Each stabilizer produces a syndrome when its measured parity differs from the expected value. We can count the number of syndromes in a $w_s \times w_s \times w_t$ window, and trigger a ray detection event if this count exceeds some threshold. Right: When a detection event is triggered, we turn off all physical qubits within the offline flag radius $r_{\text{off}}$.

Figure 7. When parts of the chip are forced offline (red patches), re-mapping enables the factory to continue operating in a new configuration, albeit at potentially reduced speed.
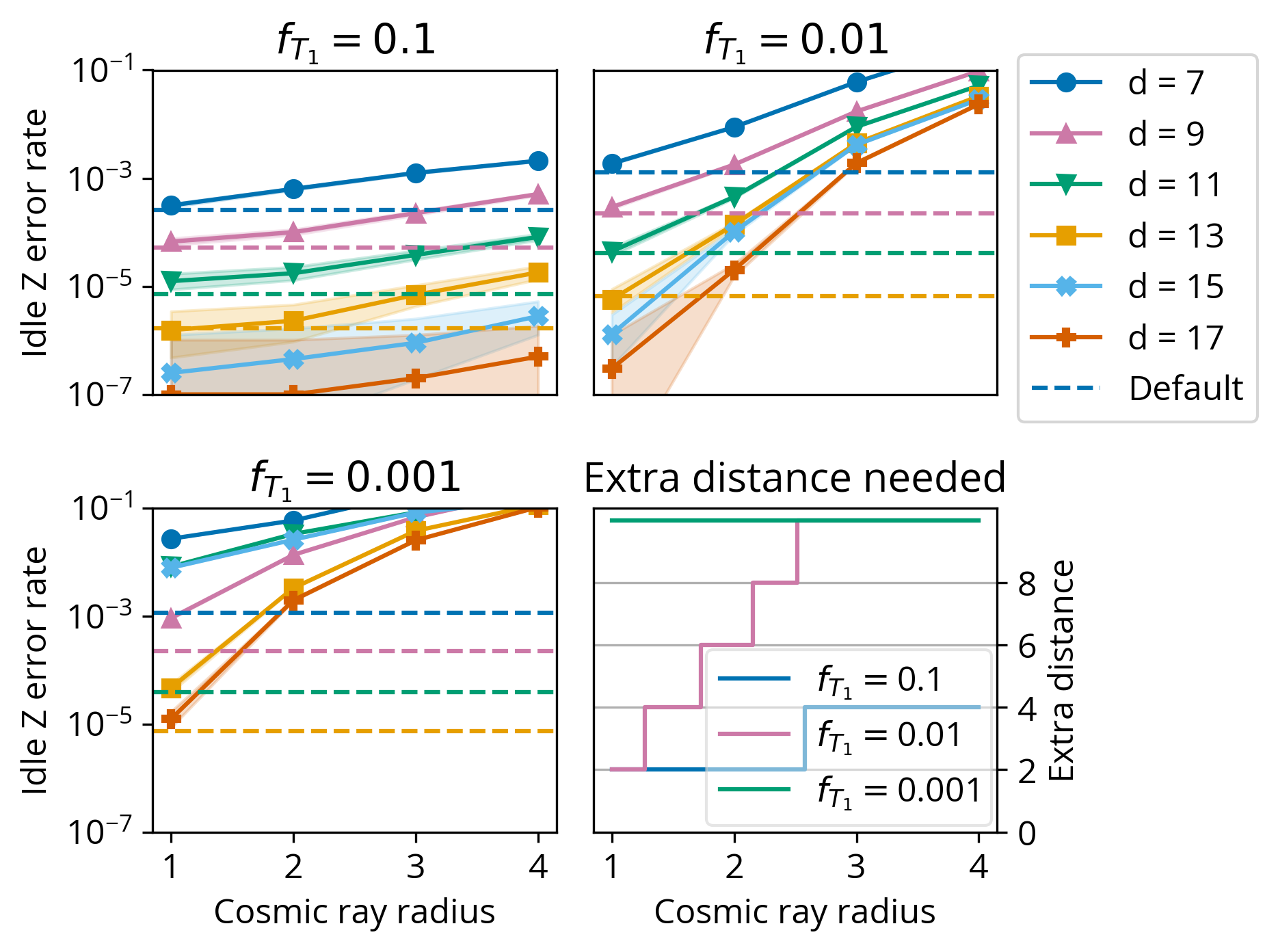
Figure 9. Extra code distance needed to tolerate Direct events of varying radius (assuming perfect decoder knowledge). Three plots show logical error rate as a function of ray radius, showing that larger rays degrade code distance more. Blue dashed line indicates $d=7$ error rate in the no-ray case. Each error rate plot shows the larger of either logical idle error rate (selected for $f_{T_1}=0.1$) or T rotation lattice surgery error rate (selected for $f_{T_1}=0.01$ and $0.001$), both obtained via Stim simulation. Bottom right: We can extract the required additional code distance for a given ray radius and strength. This determines the overhead of the Code expansion baseline.
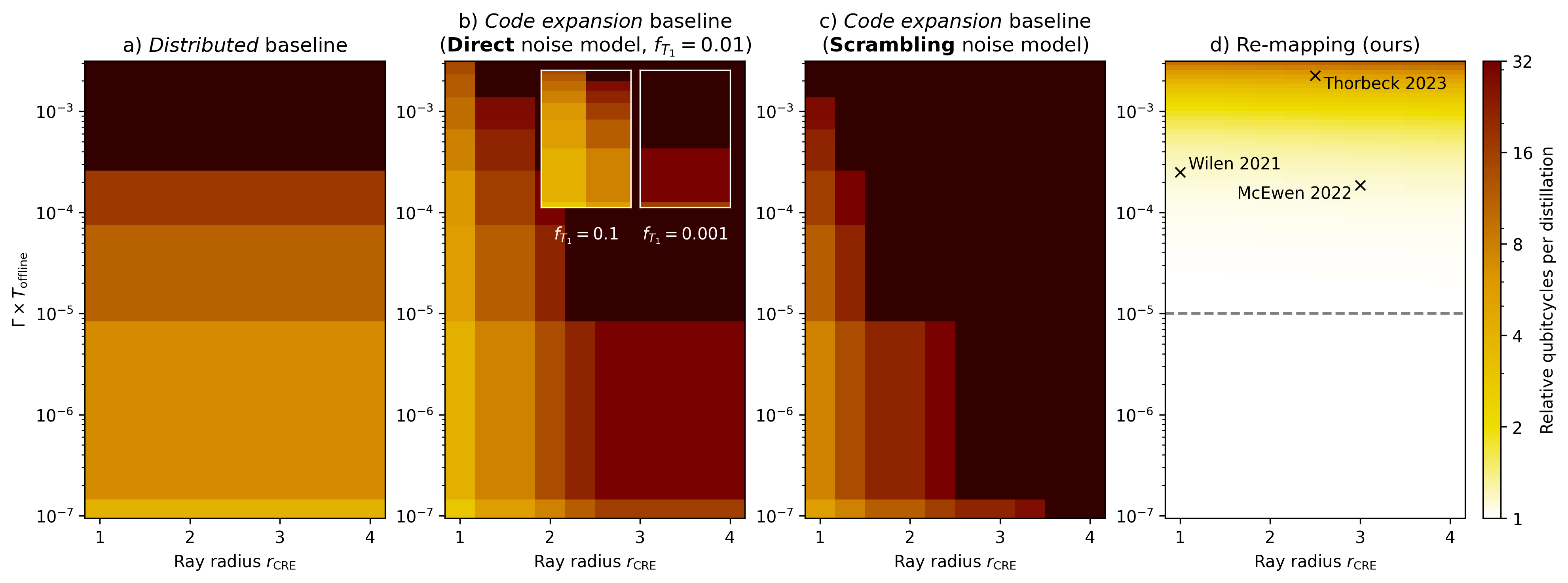
Figure 11. Quantifying the relative qubitcycle costs of cosmic ray mitigation methods in magic state factories, assuming ideal detection of ray impacts. Under ideal detection, the overheads of all methods are determined by the anomaly size (ray radius) and the value $\Gamma \times T_{\text{offline}},$ which determines the expected fraction of time that the factory is recovering from multiple ray impacts simultaneously. Our re-mapping method has significantly lower overhead across most of this parameter space. For low values of $\Gamma \times T_{\text{offline}},$ the re-mapping method incurs virtually no overhead, while for high values, the overhead is orders of magnitude lower than that of the baselines. Annotations on the rightmost plot mark the values of $\Gamma \times T_{\text{offline}}$ and $r_{\text{CRE}}$ observed in experiments [22]. [23], [44]. Scrambling model references [22] and [44] are shown assuming $T_{\text{offline}} = 1$ s. Gray dashed line incidates value of $\Gamma \times T_{\text{offline}}$ used in Figure 12.

Figure 12. Top: Distillation overhead of re-mapping method under varying detection latency for Direct model. Detection latencies are obtained from Figure 5. Ray rate value $\Gamma \times T_{\text{offline}}$ is fixed at $10^{-5}$. Bottom: Distillation overhead of re-mapping method under varying detection latency for Scrambling model. Detection latencies are obtained from Figure 6.
My Contributions
← back to jason-chadwick.com